Web 3 学习笔记 5 | 比特币的数据结构
比特币不仅是数字货币的先驱,其底层的数据结构设计也极具巧思。通过巧妙运用哈希指针和Merkle树,比特币实现了数据完整性验证和防篡改机制,为去中心化系统提供了坚实保障。本文将详细解析比特币区块链中哈希指针、Merkle树及Merkle证明的工作原理和局限性,帮助大家深入理解其底层设计逻辑。
哈希指针(Hash Pointers)
Block chain is a linked list using hash pointers.
在传统链表中,每个节点仅保存指向下一个节点的地址;而在区块链中,每个区块都使用了“哈希指针”,即在保存指针的同时,还保存了结构体的哈希值,从而实现数据内容与位置的双重绑定。
基本概念:
哈希指针 = 普通指针 + 结构体的哈希值。这种结构确保了任何数据修改都会导致哈希值变化,使得篡改行为一目了然。区块链 vs. 普通链表:
与普通链表不同,区块链使用哈希指针构建“tamper-evident log”(防篡改日志)。只要保存链中任一区块,就可以检测出之前的任一区块是否被修改。结构示意:
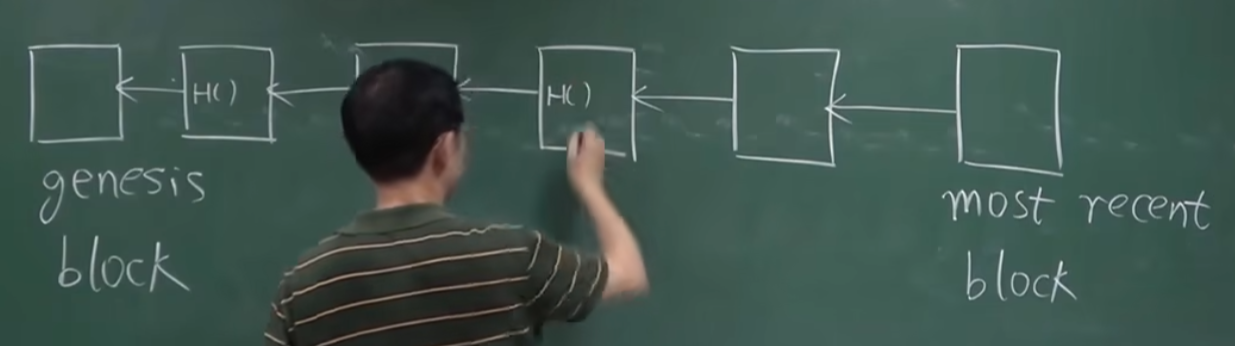
关键区块说明:
第一个区块称为创世区块(Genesis Block),作为整个链条的起点;
最新区块则被标记为Most Recent Block。
通过这种设计,每个区块都与前一个区块紧密关联,确保了区块链整体数据的一致性和安全性。
Merkle Tree(默克尔树)
Merkle树是一种树形结构,用于高效地验证大规模数据集的完整性。与传统的二叉树不同,Merkle树使用哈希指针连接节点,使得树中任一数据的微小变动都能迅速传递到根节点,从而改变整个树的根哈希。
与二叉树的区别:
普通二叉树直接存储子节点引用,而Merkle树的每个非叶子节点保存的是子节点的哈希值,这样一旦某个叶子节点(即交易信息)被篡改,经过逐层计算后,最终会导致根节点哈希发生改变。节点结构:
叶子节点(Data Blocks): 存储具体的交易信息;
其他节点(Hash Pointers): 存储子节点数据的哈希值;
根节点(Root Hash): 代表整棵树的数据完整性,只要根哈希匹配,就能证明所有数据均未被篡改。
数据块构成:
块头(Block Header): 记录哈希值及其他关键信息;
块身(Block Body): 存储交易链表或具体的交易数据。
Merkle Proof(默克尔证明)
Merkle证明是一种高效验证数据存在性的方法,它在全节点与轻节点之间起到了桥梁作用:
存储方式:
全节点(Full Node): 保存完整区块数据(
block body+block header),能提供完整的Merkle树数据;轻节点(Light Node): 只保存
block header,如钱包应用,为减少存储和计算成本,通常依赖全节点来进行数据验证。

证明交易存在(Proof of Membership / Proof of Inclusion):
轻节点向全节点请求与目标交易相关的“红色部分的哈希值”,并结合自身保存的“绿色部分哈希值”,逐层计算直至得到根哈希。若计算结果与区块中的Root Hash匹配,即可确认交易存在于Merkle树中,验证复杂度为 O(log N)。证明交易不存在(Proof of Non-Membership):
传统方法需要传输整棵树的data blocks,复杂度为 O(N)。为优化这一过程,可采用Sorted Merkle Tree(有序默克尔树),对叶子节点进行排序后通过二分查找,将验证复杂度降为 O(log N)。
哈希指针的局限性
尽管哈希指针在构建安全的数据结构方面表现优异,但也存在一些局限性:
适用范围有限:
哈希指针适用于无环数据结构,如链表和树状结构,但在有环数据结构中,由于每个节点的哈希依赖于前一个节点,可能会产生循环依赖问题,导致哈希值无法唯一确定。循环依赖问题:
一旦数据结构中出现环,哈希计算将陷入循环依赖,破坏数据完整性验证机制,因此在设计时需谨慎避免有环结构的产生。
总结
比特币利用哈希指针和Merkle树构建了一个安全、不可篡改的区块链数据结构。通过链式连接和逐层哈希验证,任何数据改动都将迅速传递至根节点,确保全网数据一致性与安全性。同时,Merkle证明机制为轻节点提供了高效的数据验证方式,尽管哈希指针在有环结构中存在局限,但整体设计为比特币系统奠定了坚实的安全基础
希望这篇分享能为你带来启发!如果你有任何问题或建议,欢迎在评论区留言,与我共同交流探讨。