[LeetCode] 每日一题 782. 变为棋盘

题目链接

题目描述

一个 n x n 的二维网络 board 仅由 0 和 1 组成 。每次移动，你能交换任意两列或是两行的位置。

返回 将这个矩阵变为  “棋盘”  所需的最小移动次数 。如果不存在可行的变换，输出 -1。

“棋盘” 是指任意一格的上下左右四个方向的值均与本身不同的矩阵。

示例输入

示例 1

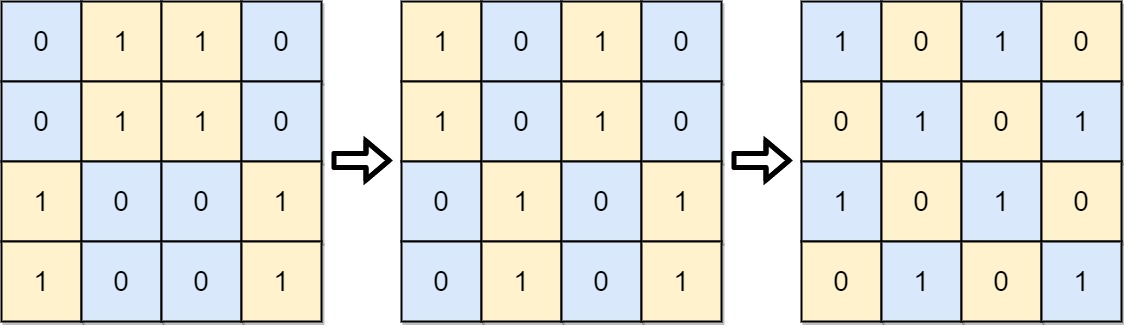
输入: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]

输出: 2

解释:一种可行的变换方式如下，从左到右：
第一次移动交换了第一列和第二列。
第二次移动交换了第二行和第三行。

示例 2

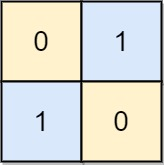
输入: board = [[0, 1], [1, 0]]

输出: 0

解释: 注意左上角的格值为0时也是合法的棋盘，也是合法的棋盘.

示例 3

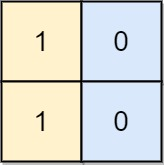
输入: board = [[1, 0], [1, 0]]

输出: -1

解释: 任意的变换都不能使这个输入变为合法的棋盘。

提示

• n == board.length

• n == board[i].length

• 2 <= n <= 30

• board[i][j] 将只包含 0或 1

题解

解题思路

为了解决这个问题，我们可以分以下几步进行：

1. 合法性检查

• 首先，一个合法的棋盘必须满足：

  1. 第一行的 0 和 1 的个数之差不能超过 1。

  2. 第一列的 0 和 1 的个数之差不能超过 1。

  3. 每一行（或列）与第一行（或列）的关系必须是完全相同或完全相反。

• 如果不满足上述任意一个条件，直接返回 -1。

2. 计算最小交换次数

为了最小化交换次数，需要分别考虑以下两种情况：

1. 调整行顺序：

   • 假设第一行满足棋盘的排列（如 0101... 或 1010...），统计与第一行不匹配的行数（错位行），通过交换行位置调整为正确排列。

   • 对于奇偶长度的矩阵，错位的行数可能有两种排列，我们取较小的交换次数。

2. 调整列顺序：

   • 同理，假设第一列满足棋盘的排列，统计与第一列不匹配的列数（错位列），通过交换列位置调整为正确排列。

最终结果是行调整和列调整的交换次数之和。

3. 特殊情况处理

• 当矩阵的大小 nnn 为奇数时，最终棋盘的排列方式是确定的（0101... 或 1010... 的数量不能相同），只需判断与之对应的交换次数。

• 当 nnn 为偶数时，两种棋盘排列方式的交换次数都可行，取较小值即可。

代码实现

以下是根据上述思路的代码实现：

class Solution {
    public int movesToChessboard(int[][] board) {
        int n = board.length;
        // 检查第一行 0 和 1 的数量是否平衡
        int cnt0 = 0;
        for (int i = 0; i < n; i++) {
            if (board[0][i] == 0) {
                cnt0++;
            }
        }
        // 如果差值超过 1，无法转换成棋盘
        if (Math.abs(cnt0 - (n - cnt0)) > 1) {
            return -1;
        }
        // 检查第一列 0 和 1 的数量是否平衡
        cnt0 = 0;
        for (int i = 0; i < n; i++) {
            if (board[i][0] == 0) {
                cnt0++;
            }
        }
        // 如果差值超过 1，无法转换成棋盘
        if (Math.abs(cnt0 - (n - cnt0)) > 1) {
            return -1;
        }
        // 检查每一行是否符合规则（与第一行完全相同或完全不同）
        for (int[] row : board) {
            boolean same = row[0] == board[0][0];
            for (int i = 0; i < n; i++) {
                // 如果不符合，无法转换成棋盘
                if ((row[i] == board[0][i]) != same) {
                    return -1;
                }
            }
        }
        int res = 0;
        // 计算第一行的最小交换次数
        int misMatch0 = 0, misMatch1 = 0;
        for (int i = 0; i < n; i++) {
            // 偶数位
            if (i % 2 == 0) {
                // 偶数位应该是 0
                if (board[0][i] != 0) {
                    misMatch0++;
                }
                // 偶数位应该是 1
                if (board[0][i] != 1) {
                    misMatch1++;
                }
            } // 奇数位
            else {
                // 奇数位应该是 1
                if (board[0][i] != 1) {
                    misMatch0++;
                }
                // 奇数位应该是 0
                if (board[0][i] != 0) {
                    misMatch1++;
                }
            }
        }
        if (n % 2 == 0) {
            res += Math.min(misMatch0, misMatch1) / 2;
        } else {
            res += (misMatch0 % 2 == 0) ? misMatch0 / 2 : misMatch1 / 2;
        }

        // 计算第一列的最小交换次数
        misMatch0 = 0;
        misMatch1 = 0;
        for (int i = 0; i < n; i++) {
            // 偶数位
            if (i % 2 == 0) {
                // 偶数位应该是 0
                if (board[i][0] != 0) {
                    misMatch0++;
                }
                // 偶数位应该是 1
                if (board[i][0] != 1) {
                    misMatch1++;
                }
            } // 奇数位
            else {
                // 奇数位应该是 1
                if (board[i][0] != 1) {
                    misMatch0++;
                }
                // 奇数位应该是 0
                if (board[i][0] != 0) {
                    misMatch1++;
                }
            }
        }
        if (n % 2 == 0) {
            res += Math.min(misMatch0, misMatch1) / 2;
        } else {
            res += (misMatch0 % 2 == 0) ? misMatch0 / 2 : misMatch1 / 2;
        }
        return res;
    }
}

总结

1. 通过合法性检查，快速过滤无法变成棋盘的矩阵。

2. 分别计算行和列的最小交换次数，解决错位问题。

3. 考虑矩阵大小为奇偶数时的特殊情况，确保结果正确。

4. 时间复杂度为 O(n^2)，适用于大部分情况。

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。