[LeetCode] 每日一题 2614. 对角线上的质数

题目链接

https://leetcode.cn/problems/prime-in-diagonal

题目描述

给你一个下标从 0 开始的二维整数数组 nums 。

返回位于 nums 至少一条 对角线 上的最大 质数 。如果任一对角线上均不存在质数，返回 0 。

注意：

• 如果某个整数大于 1 ，且不存在除 1 和自身之外的正整数因子，则认为该整数是一个质数。

• 如果存在整数 i ，使得 nums[i][i] = val 或者 nums[i][nums.length - i - 1]= val ，则认为整数 val 位于 nums 的一条对角线上。

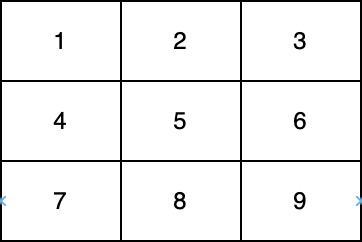
在上图中，一条对角线是 [1,5,9] ，而另一条对角线是 [3,5,7] 。

示例输入

示例 1

输入：nums = [[1,2,3],[5,6,7],[9,10,11]]
输出：11
解释：数字 1、3、6、9 和 11 是所有 "位于至少一条对角线上" 的数字。由于 11 是最大的质数，故返回 11 。

示例 2

输入：nums = [[1,2,3],[5,17,7],[9,11,10]]
输出：17
解释：数字 1、3、9、10 和 17 是所有满足"位于至少一条对角线上"的数字。由于 17 是最大的质数，故返回 17 。

提示

• 1 <= nums.length <= 300

• nums.length == numsi.length

• 1 <= nums[i][j] <= 4*10^6

解题思路

本题要求在二维数组 nums 的两条对角线上找到最大的质数。核心思路是遍历对角线上的所有元素，判断是否为质数，并记录最大值。

具体步骤如下：

1. 由于 nums 可能不是方阵，因此遍历的次数应取 min(行数, 列数)，以防越界（本题限制了nums.length == numsi.length ，所以这一点无所谓）

2. 依次检查主对角线（nums[i][i]）和副对角线（nums[i][nums.length - i - 1]）上的数是否为质数

3. 采用常见的试除法判断质数：

   • 质数必须大于 1。

   • 只需遍历到 sqrt(num) 即可，减少计算量

4. 记录过程中遇到的最大质数，最终返回结果

代码实现

class Solution {
    public int diagonalPrime(int[][] nums) {
        int n = Math.min(nums.length, nums[0].length);
        int ans = 0;
        for (int i = 0; i < n; i++) {
            if (isPrime(nums[i][i])) {
                ans = Math.max(ans, nums[i][i]);
            }
            if (isPrime(nums[i][nums.length - i - 1])) {
                ans = Math.max(ans, nums[i][nums.length - i - 1]);
            }
        }
        return ans;
    }

    private boolean isPrime(int num) {
        if (num == 1) {
            return false;
        }
        int temp = 2;
        while (temp * temp <= num) {
            if (num % temp == 0) {
                return false;
            }
            temp++;
        }
        return true;
    }
}

复杂度分析

• 时间复杂度：O(n√m)，其中 n 是对角线元素的个数，m 是对角线元素的最大值。在最坏情况下，每个元素都要进行质数判定，而判定质数的复杂度为 O(√m)。

• 空间复杂度：O(1)，只使用了常数级的额外空间。

总结

本题的关键在于遍历对角线并高效判断质数，可以使用试除法减少计算量。核心优化点在于 isPrime 只需检查到 sqrt(num)，大幅优化效率。整体逻辑清晰，直接遍历即可完成求解

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。