[LeetCode] 每日一题 935. 骑士拨号器

题目链接

题目描述

象棋骑士有一个独特的移动方式，它可以垂直移动两个方格，水平移动一个方格，或者水平移动两个方格，垂直移动一个方格(两者都形成一个 L 的形状)。

象棋骑士可能的移动方式如下图所示:

我们有一个象棋骑士和一个电话垫，如下所示，骑士只能站在一个数字单元格上(即蓝色单元格)。

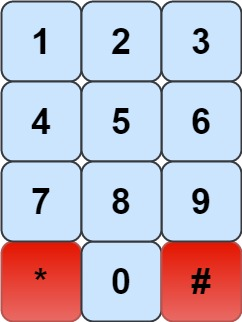
给定一个整数 n，返回我们可以拨多少个长度为 n 的不同电话号码。

你可以将骑士放置在任何数字单元格上，然后你应该执行 n - 1 次移动来获得长度为 n 的号码。所有的跳跃应该是有效的骑士跳跃。

因为答案可能很大，所以输出答案模 109 + 7.

示例输入

示例 1

输入：n = 1

输出：10

解释：我们需要拨一个长度为1的数字，所以把骑士放在10个单元格中的任何一个数字单元格上都能满足条件。

示例 2

输入：n = 2

输出：20

解释：我们可以拨打的所有有效号码为[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

示例 3

输入：n = 3131

输出：136006598

解释：注意取模

提示

• 1 <= n <= 5000

题解

思路解析

1. 建模骑士的跳跃规则：

   • 每个数字对应一组合法的跳跃位置。例如：

     • 数字 0 可跳到 4, 6。

     • 数字 1 可跳到 6, 8。

   • 我们可以用一个二维数组表示跳跃关系。

2. 问题的动态规划转化：

   • 用 dfs(n, i) 表示从数字 i 开始，跳跃 n 次后生成的电话号码数量。

   • 状态转移方程为：
     dfs(n,i)=∑j∈move[i]dfs(n−1,j)
     意思是：从当前数字 i 开始的路径数等于所有可以跳跃到 j 的路径数之和。

   • 递归的终止条件为：

     • 如果剩余步数 n == 0，返回 1（表示形成了一个号码）。

   • 使用记忆化数组 memory 缓存计算结果，避免重复计算。

3. 初始状态：

   • 骑士可以从任何数字开始，因此需要累加从每个数字出发的结果。

4. 结果取模：

   • 因为路径数可能很大，所有的中间计算和最终结果均需模 10^9+7。

代码实现

class Solution {
    // 定义骑士跳跃的规则
    int[][] move = { 
        { 4, 6 }, { 6, 8 }, { 7, 9 }, { 4, 8 }, { 0, 3, 9 }, {}, 
        { 0, 1, 7 }, { 2, 6 }, { 1, 3 }, { 2, 4 } 
    };

    public int knightDialer(int n) {
        // 初始化记忆化数组
        int[][] memory = new int[n][10]; 
        if (n == 1) {
            return 10;
        }
        int res = 0;
        // 遍历从每个数字开始的路径
        for (int i = 0; i < 10; i++) {
            res = (res + dfs(n - 1, i, memory)) % 1000000007;
        }
        return res;
    }

    // 深度优先搜索 + 记忆化
    int dfs(int n, int i, int[][] memory) {
        if (n == 0) {
            return 1; // 递归终止条件
        }
        if (memory[n][i] > 0) {
            return memory[n][i]; // 缓存命中
        }
        int res = 0;
        // 计算从当前数字跳跃的路径数
        for (int j : move[i]) {
            res = (res + dfs(n - 1, j, memory)) % 1000000007;
        }
        memory[n][i] = res; // 保存结果到缓存
        return res;
    }
}

复杂度分析

• 时间复杂度：

  • 理论上每个数字最多有 8 个合法跳跃，搜索深度为 n，总时间复杂度为 O(10⋅n⋅8)，但由于使用了记忆化优化，实际复杂度大幅降低为 O(10⋅n)。

• 空间复杂度：

  • 记忆化数组占用 O(10⋅n) 的空间。

总结

• 本题通过骑士跳跃构造合法的电话号码，结合记忆化搜索，解决了路径重复计算问题。

• 采用动态规划的思路，将递归与缓存结合，优化了时间复杂度。

• 在实际问题中，这种思路非常适用于处理多步跳跃、网格遍历等类似问题，具有很强的通用性。

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。