[LeetCode] 每日一题 3001. 捕获黑皇后需要的最少移动次数

题目链接

题目描述

现有一个下标从 1 开始的 8 x 8 棋盘，上面有 3 枚棋子。

给你 6 个整数 a 、b 、c 、d 、e 和 f ，其中：

• (a, b) 表示白色车的位置。

• (c, d) 表示白色象的位置。

• (e, f) 表示黑皇后的位置。

假定你只能移动白色棋子，返回捕获黑皇后所需的最少移动次数。

请注意：

• 车可以向垂直或水平方向移动任意数量的格子，但不能跳过其他棋子。

• 象可以沿对角线方向移动任意数量的格子，但不能跳过其他棋子。

• 如果车或象能移向皇后所在的格子，则认为它们可以捕获皇后。

• 皇后不能移动。

示例输入

示例 1

输入：a = 1, b = 1, c = 8, d = 8, e = 2, f = 3

输出：2

解释：将白色车先移动到 (1, 3) ，然后移动到 (2, 3) 来捕获黑皇后，共需移动 2 次。
由于起始时没有任何棋子正在攻击黑皇后，要想捕获黑皇后，移动次数不可能少于 2 次。

示例 2

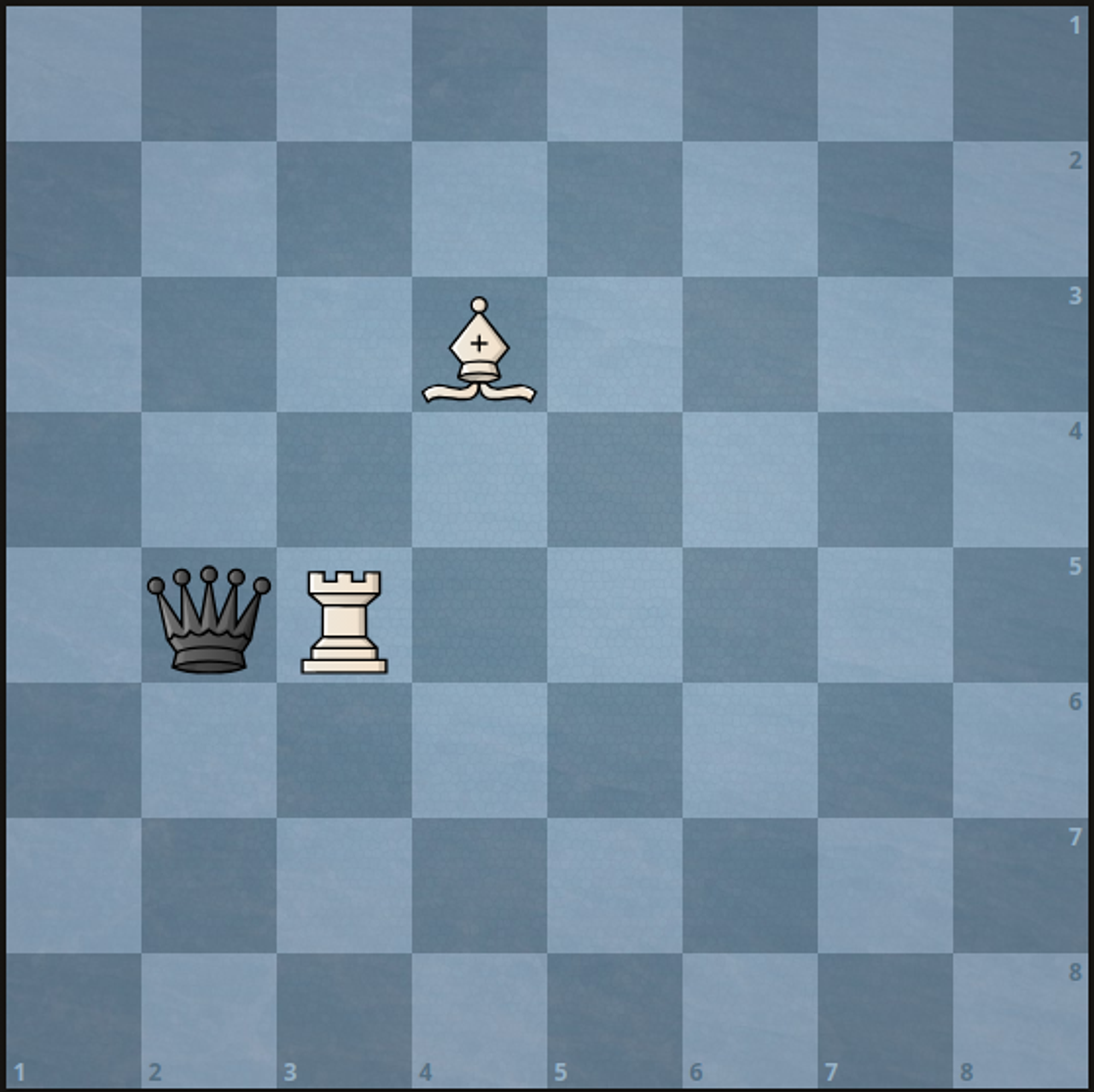
输入：a = 5, b = 3, c = 3, d = 4, e = 5, f = 2

输出：1

解释：可以通过以下任一方式移动 1 次捕获黑皇后：
- 将白色车移动到 (5, 2) 。
- 将白色象移动到 (5, 2) 。

提示

• 1 <= a, b, c, d, e, f <= 8

• 两枚棋子不会同时出现在同一个格子上。

题解

题目理解

在一个标准的 8x8 棋盘上，给定三个棋子的初始位置：白色车（a, b）、白色象（c, d）以及黑皇后（e, f）。我们的目标是计算最少的移动次数，捕获黑皇后。我们可以通过操作白色车和白色象来捕获黑皇后，规则如下：

• 车：可以在水平或垂直方向上移动，任意格数，但不能跨越其他棋子。

• 象：可以在对角线方向上移动，任意格数，但也不能跨越其他棋子。

若车或象能到达黑皇后所在的格子，便算作成功捕获。根据不同情况，我们需要判断最少的移动次数。

核心思路

此题的核心思路是根据车和象的移动规则，分别判断它们能否在一次移动中捕获黑皇后。如果它们不能直接捕获黑皇后，则需要两步。

1. 车的捕获规则：

   • 如果车和皇后处在同一行或同一列，并且车和皇之间没有障碍物（象阻挡），则车可以捕获皇后。

2. 象的捕获规则：

   • 如果象和皇后处于同一条对角线上，并且它们之间没有其他障碍物（如车阻挡），则象可以捕获皇后。

3. 无法直接捕获的情况：

   • 如果车和象都不能直接捕获皇后，则需要两步，首先移动到合适的位置，然后再捕获。

具体实现

我们通过两个辅助方法来分别判断车和象是否能捕获皇后：

1. canCaptureWithRook：判断车是否能捕获皇后。车必须与皇后在同一行或列，并且路径中没有象阻挡。

2. canCaptureWithBishop：判断象是否能捕获皇后。象必须与皇后处于同一条对角线上，且路径中没有车阻挡。

代码实现

class Solution {
    public int minMovesToCaptureTheQueen(int a, int b, int c, int d, int e, int f) {
        // 判断用车吃皇后的情况
        if (canCaptureWithRook(a, b, c, d, e, f) || canCaptureWithBishop(a, b, c, d, e, f)) {
            return 1;  // 可以在一次移动中捕获
        }
        
        // 如果不能通过车或象吃到皇后，则需要两步
        return 2;
    }

    // 判断用车吃皇后的情况
    boolean canCaptureWithRook(int a, int b, int c, int d, int e, int f) {
        // 车和皇后在同一行且中间没有象
        if (a == e && (c != a || d <= Math.min(b, f) || d >= Math.max(b, f))) {
            return true;
        }
        // 车和皇后在同一列且中间没有象
        if (b == f && (d != b || c <= Math.min(a, e) || c >= Math.max(a, e))) {
            return true;
        }
        return false;
    }

    // 判断用象吃皇后的情况
    boolean canCaptureWithBishop(int a, int b, int c, int d, int e, int f) {
        // 象和皇后是否在同一条对角线
        if (Math.abs(c - e) != Math.abs(d - f)) {
            return false;
        }
        // 对角线中没有车
        if (((c - e) * (b - f) == (a - e) * (d - f) && a >= Math.min(c, e) && a <= Math.max(c, e))) {
            return false;
        }
        return true;
    }
}

代码解析

• minMovesToCaptureTheQueen：

  • 如果车或象可以在一步内捕获皇后，返回 1；否则返回 2，表示至少需要两步。

• canCaptureWithRook：

  • 首先判断车与皇后是否在同一行 a == e 或同一列 b == f。

  • 如果车与皇后在同一行或列，并且路径中没有象，返回 true，表示车可以捕获皇后。

• canCaptureWithBishop：

  • 通过判断象和皇后是否在同一对角线 Math.abs(c - e) == Math.abs(d - f)。

  • 如果在同一对角线且路径中没有车阻挡，返回 true，表示象可以捕获皇后。

时间复杂度

• 每个方法的时间复杂度为 O(1)，因为我们只是做了常数次的数学计算和逻辑判断。

• 因此，整个算法的时间复杂度为 O(1)。

空间复杂度

• 空间复杂度为 O(1)，只使用了少量的常数空间来存储临时变量。

总结

通过判断车和象是否可以直接捕获皇后，我们将问题分解成了两个简单的判断。代码通过清晰的逻辑结构，分别处理车和象的捕获情况，最后根据条件返回最小的移动次数。这样既能保证代码的简洁性，又能提高可读性。

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。