[LeetCode] 每日一题 2056. 棋盘上有效移动组合的数目
题目链接
题目描述
有一个 8 x 8 的棋盘,它包含 n 个棋子(棋子包括车,后和象三种)。给你一个长度为 n 的字符串数组 pieces ,其中 pieces[i] 表示第 i 个棋子的类型(车,后或象)。除此以外,还给你一个长度为 n 的二维整数数组 positions ,其中 positions[i] = [ri, ci] 表示第 i 个棋子现在在棋盘上的位置为 (ri, ci) ,棋盘下标从 1 开始。
棋盘上每个棋子都可以移动 至多一次 。每个棋子的移动中,首先选择移动的 方向 ,然后选择 移动的步数 ,同时你要确保移动过程中棋子不能移到棋盘以外的地方。棋子需按照以下规则移动:
车可以 水平或者竖直 从
(r, c)沿着方向(r+1, c),(r-1, c),(r, c+1)或者(r, c-1)移动。后可以 水平竖直或者斜对角 从
(r, c)沿着方向(r+1, c),(r-1, c),(r, c+1),(r, c-1),(r+1, c+1),(r+1, c-1),(r-1, c+1),(r-1, c-1)移动。象可以 斜对角 从
(r, c)沿着方向(r+1, c+1),(r+1, c-1),(r-1, c+1),(r-1, c-1)移动。
移动组合 包含所有棋子的 移动 。每一秒,每个棋子都沿着它们选择的方向往前移动 一步 ,直到它们到达目标位置。所有棋子从时刻 0 开始移动。如果在某个时刻,两个或者更多棋子占据了同一个格子,那么这个移动组合 不有效 。
请你返回 有效 移动组合的数目。
注意:
初始时,不会有两个棋子 在 同一个位置 。
有可能在一个移动组合中,有棋子不移动。
如果两个棋子 直接相邻 且两个棋子下一秒要互相占据对方的位置,可以将它们在同一秒内 交换位置 。
示例输入
示例 1
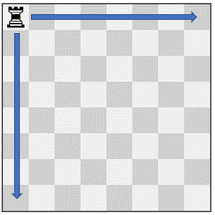
输入:pieces = ["rook"], positions = [[1,1]]
输出:15
解释:上图展示了棋子所有可能的移动。示例 2
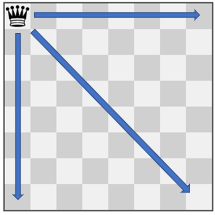
输入:pieces = ["queen"], positions = [[1,1]]
输出:22
解释:上图展示了棋子所有可能的移动。示例 3
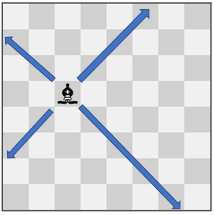
输入:pieces = ["bishop"], positions = [[4,3]]
输出:12
解释:上图展示了棋子所有可能的移动。示例 4
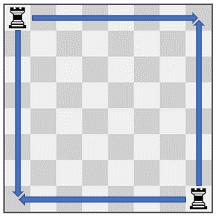
输入:pieces = ["rook","rook"], positions = [[1,1],[8,8]]
输出:223
解释:每个车有 15 种移动,所以总共有 15 * 15 = 225 种移动组合。
但是,有两个是不有效的移动组合:
- 将两个车都移动到 (8, 1) ,会导致它们在同一个格子相遇。
- 将两个车都移动到 (1, 8) ,会导致它们在同一个格子相遇。
所以,总共有 225 - 2 = 223 种有效移动组合。
注意,有两种有效的移动组合,分别是一个车在 (1, 8) ,另一个车在 (8, 1) 。
即使棋盘状态是相同的,这两个移动组合被视为不同的,因为每个棋子移动操作是不相同的。示例 5

输入:pieces = ["queen","bishop"], positions = [[5,7],[3,4]]
输出:281
解释:总共有 12 * 24 = 288 种移动组合。
但是,有一些不有效的移动组合:
- 如果后停在 (6, 7) ,它会阻挡象到达 (6, 7) 或者 (7, 8) 。
- 如果后停在 (5, 6) ,它会阻挡象到达 (5, 6) ,(6, 7) 或者 (7, 8) 。
- 如果象停在 (5, 2) ,它会阻挡后到达 (5, 2) 或者 (5, 1) 。
在 288 个移动组合当中,281 个是有效的。提示
n == pieces.lengthn == positions.length1 <= n <= 4pieces只包含字符串"rook","queen"和"bishop"。棋盘上最多只有一个后。
1 <= ri, ci <= 8每一个
positions[i]互不相同。
题解
题目理解
我们在一个 8x8 的棋盘上,有若干个棋子。每个棋子有一个初始位置,可以沿着特定的方向进行多步合法移动。要求计算这些棋子在给定的初始位置和移动规则下,所有合法的移动组合的数量。合法的移动组合是指这些棋子的移动过程中不会发生重叠,即不会有任何两个棋子在同一时刻处于相同的格子。
核心思路
这个问题的核心在于回溯(backtracking)和剪枝。我们可以通过以下几个步骤来解决问题:
预处理每个棋子的所有合法移动:
每个棋子的合法移动受限于其初始位置、可用的移动方向以及步数。我们首先根据每个棋子的类型(车、象、皇后等)和其初始位置,预先计算出该棋子在所有方向上可能的合法移动路径。
回溯暴力枚举所有合法的移动组合:
对于每个棋子,我们枚举它所有的合法移动路径。如果某条路径与前面已选择的棋子发生冲突(即棋子在相同的时刻重叠),则不继续选择该路径。
如果当前棋子的所有路径都没有冲突,我们就递归到下一个棋子,直到所有棋子的路径都被选定。
剪枝优化:
在回溯过程中,如果当前棋子的路径与之前棋子发生了冲突,立即跳过该路径。这样可以避免不必要的递归,提升效率。
具体实现
预处理合法路径:
对于每个棋子,生成其可能的移动路径,包括原地不动和沿着每个方向的多步移动。
路径冲突判断:
定义一个
crashed方法,判断两个棋子是否在相同的时间步内重叠。具体地,我们通过模拟每个棋子按步数移动来判断是否发生重叠。
回溯算法:
使用回溯算法来暴力枚举每个棋子的所有合法路径。如果某个路径与之前的路径冲突,则剪枝,跳过当前路径。
class Solution {
// 每种棋子的移动方向
static Map<String, int[][]> piecesDir = Map.of(
"rook", new int[][] { { 1, 0 }, { -1, 0 }, { 0, 1 }, { 0, -1 } },
"bishop", new int[][] { { 1, 1 }, { 1, -1 }, { -1, 1 }, { -1, -1 } },
"queen", new int[][] { { 1, 0 }, { -1, 0 }, { 0, 1 }, { 0, -1 }, { 1, 1 }, { 1, -1 }, { -1, 1 }, { -1, -1 } }
);
public int countCombinations(String[] pieces, int[][] positions) {
int n = pieces.length;
List<List<Path>> allPaths = new ArrayList<>();
// 为每个棋子生成所有的合法路径
for (int i = 0; i < n; i++) {
allPaths.add(genPath(piecesDir.get(pieces[i]), positions[i][0], positions[i][1]));
}
Path[] move = new Path[n]; // 当前棋子的移动路径
return dfs(0, n, allPaths, move);
}
// 生成每个棋子在特定方向上的所有合法路径
private List<Path> genPath(int[][] dirs, int x, int y) {
List<Path> paths = new ArrayList<>();
// 原地不动
paths.add(new Path(x, y, 0, 0, 0));
for (int[] dir : dirs) {
int px = x + dir[0];
int py = y + dir[1];
for (int step = 1; px > 0 && py > 0 && px <= 8 && py <= 8; step++) {
paths.add(new Path(x, y, dir[0], dir[1], step));
px += dir[0];
py += dir[1];
}
}
return paths;
}
private int dfs(int i, int n, List<List<Path>> allPaths, Path[] move) {
if (i == n) {
return 1; // 所有棋子都有合法路径
}
int res = 0;
// 枚举当前棋子的所有合法路径
for (Path path : allPaths.get(i)) {
boolean skip = false;
for (int j = 0; j < i; j++) {
if (path.crashed(move[j])) {
skip = true; // 路径冲突,跳过
break; // 一旦发现冲突,跳出内层循环
}
}
if (skip) {
continue; // 跳过当前路径,继续检查下一个路径
}
move[i] = path; // 记录当前棋子的路径
res += dfs(i + 1, n, allPaths, move); // 递归检查下一个棋子的路径
}
return res;
}
// 定义棋子的路径
static class Path {
int x;
int y;
int dx;
int dy;
int step;
Path(int x, int y, int dx, int dy, int step) {
this.x = x;
this.y = y;
this.dx = dx;
this.dy = dy;
this.step = step;
}
// 判断是否与其它路径相冲突
boolean crashed(Path other) {
int x1 = x, y1 = y;
int x2 = other.x, y2 = other.y;
for (int i = 0; i < Math.max(step, other.step); i++) {
// 模拟棋子移动
if (i < step) {
x1 += dx;
y1 += dy;
}
if (i < other.step) {
x2 += other.dx;
y2 += other.dy;
}
if (x1 == x2 && y1 == y2) {
return true;
}
}
return false;
}
}
}希望这篇分享能为你带来启发!如果你有任何问题或建议,欢迎在评论区留言,与我共同交流探讨。