[LeetCode] 每日一题 1706. 球会落何处

题目链接

https://leetcode.cn/problems/where-will-the-ball-fall

题目描述

用一个大小为 m x n 的二维网格 grid 表示一个箱子。你有 n 颗球。箱子的顶部和底部都是开着的。

箱子中的每个单元格都有一个对角线挡板，跨过单元格的两个角，可以将球导向左侧或者右侧。

• 将球导向右侧的挡板跨过左上角和右下角，在网格中用 1 表示。

• 将球导向左侧的挡板跨过右上角和左下角，在网格中用 -1 表示。

在箱子每一列的顶端各放一颗球。每颗球都可能卡在箱子里或从底部掉出来。如果球恰好卡在两块挡板之间的 "V" 形图案，或者被一块挡导向到箱子的任意一侧边上，就会卡住。

返回一个大小为 n 的数组 answer ，其中 answer[i] 是球放在顶部的第 i 列后从底部掉出来的那一列对应的下标，如果球卡在盒子里，则返回 -1 。

示例输入

示例 1

输入：grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]
输出：[1,-1,-1,-1,-1]
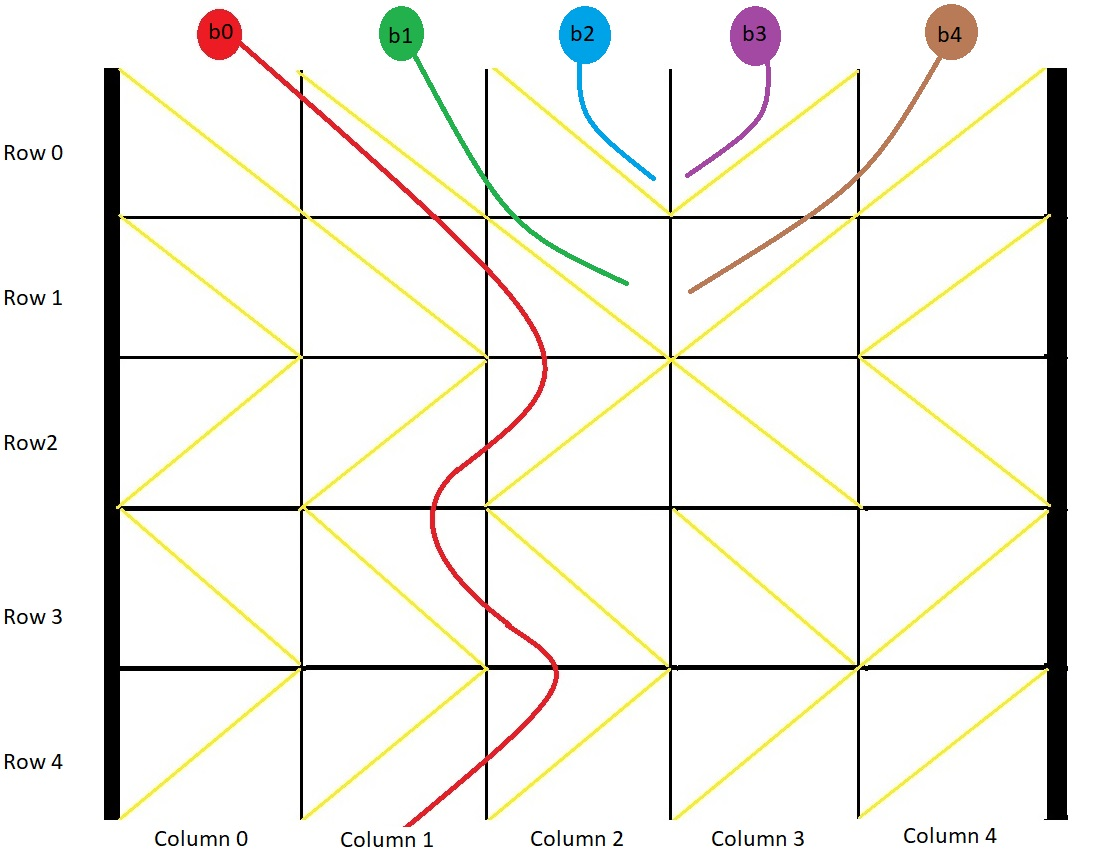
解释：示例如图：
b0 球开始放在第 0 列上，最终从箱子底部第 1 列掉出。
b1 球开始放在第 1 列上，会卡在第 2、3 列和第 1 行之间的 "V" 形里。
b2 球开始放在第 2 列上，会卡在第 2、3 列和第 0 行之间的 "V" 形里。
b3 球开始放在第 3 列上，会卡在第 2、3 列和第 0 行之间的 "V" 形里。
b4 球开始放在第 4 列上，会卡在第 2、3 列和第 1 行之间的 "V" 形里。

示例 2

输入：grid = [[-1]]
输出：[-1]
解释：球被卡在箱子左侧边上。

示例 3

输入：grid = [[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1],[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1]]
输出：[0,1,2,3,4,-1]

提示

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 100

• grid[i][j] 为 1 或 -1

解题思路

今天的题目要求我们模拟小球从箱子顶部下落的过程。在模拟过程中，小球根据挡板的方向移动。如果在某个位置被卡住，则返回 -1，否则返回最终小球的下落位置。题目条件直观，而下落过程中可能会遇到几种卡住的情况，我们可以通过合理的条件判断来处理这些特殊情况

我的思路是直接按照题意进行模拟。已知小球一开始不会被卡住，且只要小球没有卡住，它就会继续下落。因此，我通过逐行模拟每颗小球的下落过程。在下落过程中，小球有四种可能会被卡住的情况：

• 小球在最左边，而挡板也让小球向左移动

• 小球在最右边，而挡板让小球向右移动

• 小球当前位置的挡板指向左侧，同时左边的挡板指向右侧，导致小球卡住

• 小球当前位置的挡板指向右侧，同时右边的挡板指向左侧，导致小球卡住

我觉得这道题的有趣之处在于判断条件的设计。在模拟小球下落的过程中，很多时候我们容易陷入先判断是否可以移动，再进行下落的思维方式，这会让逻辑变得复杂且难以理解。而一个更简洁的做法是：先假设小球能够顺利下落，进行位置移动，然后再检查这个移动是否合法

这种做法避免了过早地做出判断，而是直接利用小球当前位置进行模拟，后续再验证该移动是否合法。通过这种方式，我们将判断和移动过程分开，代码显得更简洁易懂。具体来说，我们在模拟每个小球下落时，先按照挡板的方向更新小球的位置，然后判断移动后的位置是否合法。如果某次移动导致小球卡住，就返回 -1，否则继续模拟下去，直到小球顺利下落到底部或卡住为止

这种思路在模拟类题目中非常常见，能够清晰地处理多种情况，同时避免了过于复杂的条件判断，使得整体代码更加清晰和高效

代码实现

class Solution {
    public int[] findBall(int[][] grid) {
        int n = grid[0].length;
        int[] ans = new int[n];
        for (int i = 0; i < n; i++) {
            // 记录结果位置
            int result = i;
            // 按行模拟小球位置
            for (int[] row : grid) {
                int dir = row[result];
                result += dir;
                // 如果小球下一个位置卡墙，或者下一个位置挡板方向与当前不同，说明被卡住无法出来
                if (result < 0 || result >= n || dir != row[result]) {
                    result = -1;
                    break;
                }
            }
            ans[i] = result;
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：O(m * n)，其中 m 是 grid 的行数，n 是每行的列数。每颗小球都需要模拟其下落过程，这意味着每颗小球最多需要遍历所有的行。因此时间复杂度为 O(m * n)

• 空间复杂度：O(n)，我们需要一个长度为 n 的数组来存储每颗小球的最终落点位置，因此空间复杂度为 O(n)

总结

这道题的核心在于如何模拟小球的下落过程，尤其是如何判断小球是否会被卡住。在我做这道题时，发现提前判断每次小球能否合法下落会增加不必要的复杂度，反而采用先假设小球能顺利下落、然后再验证是否合法的思路，使得代码结构更加简洁和高效

通过这种模拟方式，我们避免了繁琐的条件判断，让整体逻辑变得更加清晰。对于此类模拟移动的题目来说，这种方法是常见且高效的

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。