[LeetCode] 每日一题 1552. 两球之间的磁力

题目链接

https://leetcode.cn/problems/magnetic-force-between-two-balls

题目描述

在代号为 C-137 的地球上，Rick 发现如果他将两个球放在他新发明的篮子里，它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子，第 i 个篮子的位置在 position[i] ，Morty 想把 m 个球放到这些篮子里，使得任意两球间 最小磁力 最大。

已知两个球如果分别位于 x 和 y ，那么它们之间的磁力为 |x - y| 。

给你一个整数数组 position 和一个整数 m ，请你返回最大化的最小磁力。

示例输入

示例 1

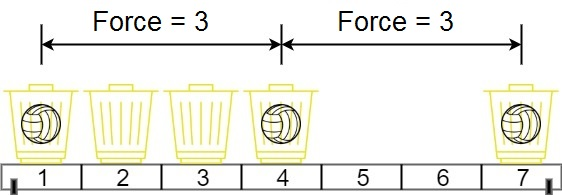
输入：position = [1,2,3,4,7], m = 3
输出：3
解释：将 3 个球分别放入位于 1，4 和 7 的三个篮子，两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。

示例 2

输入：position = [5,4,3,2,1,1000000000], m = 2
输出：999999999
解释：我们使用位于 1 和 1000000000 的篮子时最小磁力最大。

提示

• n == position.length

• 2 <= n <= 10^5

• 1 <= position[i] <= 10^9

• 所有 position 中的整数 互不相同 。

• 2 <= m <= position.length

解题思路

今天的题目和前几天的一些题目有点类似，都是利用逆向思维，首先确定目标——即在满足条件下最大化最小的磁力。为了高效地查找最优解，我们可以使用二分法

首先，我们将 position 数组排序，这样便于处理球的位置。接着，我们通过二分法在可能的磁力区间内进行查找，具体来说，二分的区间是 [1, position[position.length - 1] - position[0]]，即最小磁力为 1，最大磁力为数组中的最大差值。然后，在每次二分时，检查当前磁力 mid 是否能放置足够的球。若可以，则尝试增大磁力，反之则减小

通过这种方式，我们可以高效地找到最大化的最小磁力

代码实现

class Solution {
    public int maxDistance(int[] position, int m) {
        Arrays.sort(position);
        int ans = position[position.length - 1] - position[0];
        int left = 1, right = position[position.length - 1] - position[0];
        while (left <= right) {
            int mid = (left + right) / 2;
            if (check(position, m, mid)) {
                left = mid + 1;
                ans = mid;
            } else {
                right = mid - 1;
            }
        }
        return ans;
    }

    private boolean check(int[] position, int m, int distance) {
        int pre = position[0], count = 1;
        for (int i = 1; i < position.length; i++) {
            if (position[i] - pre >= distance) {
                count++;
                pre = position[i];
            }
        }
        return count >= m;
    }
}

复杂度分析

• 时间复杂度：二分法的区间大小是 position[position.length - 1] - position[0]，设为 d。在每次二分中，我们需要遍历 position 数组进行检查，检查过程的时间复杂度是 O(n)，其中 n 是 position 数组的长度。因此，整体的时间复杂度是 O(n * log d)，其中 d 是 position 数组的最大差值

• 空间复杂度：O(1)，除了输入的数组，我们只用了常数的额外空间

总结

今天这道题主要考察了二分法在区间查找中的应用。通过逆向思维，转化为在一个区间内找到能够满足条件的最大值。此题的难点在于如何将问题建模为一个区间问题并使用二分法高效求解

通过二分法和检查函数相结合，我们能够在较短的时间内找到最优解，避免了直接模拟的低效方式

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。