[LeetCode] 每日一题 790. 多米诺和托米诺平铺（动态规划）

题目描述

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 "L" 的托米诺形。两种形状都可以旋转。

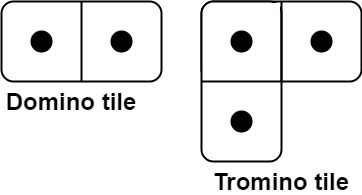
给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

题目链接

https://leetcode.cn/problems/domino-and-tromino-tiling

示例输入

示例 1

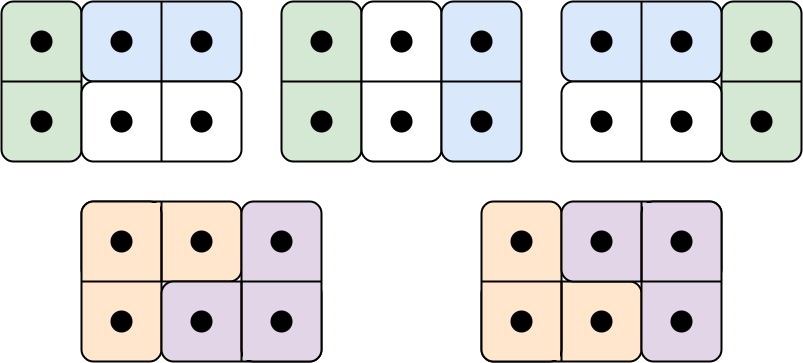
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。

示例 2

输入: n = 1
输出: 1

提示

• 1 <= n <= 1000

解题思路

这道题属于典型的动态规划问题，题干中提到的“2×n 的面板”和“多种拼法”的组合方式，很容易让人联想到类似“跳楼梯”问题，即状态转移依赖于前面的解法。

我们可以设 dp[i] 表示平铺 2 × i 面板的方法数。观察一些小的 n 值可以总结出状态转移公式：

• dp[0] = 1，代表空板子也算一种铺法；

• dp[1] = 1，只能用一块 2×1 的竖着的多米诺；

• dp[2] = 2，可以横着放两个多米诺，或者竖着放两个；

• 从 i >= 3 开始，考虑最后一列拼法，可以从：

  • dp[i - 1] 直接延续（补一个竖的多米诺）；

  • dp[i - 2] 的基础上补两个横向多米诺；

  • dp[i - 3] 的基础上补上一个托米诺（L 形旋转）再补一块填满缺口的多米诺，共两种托米诺构型，产生乘 2 的效果

所以有dp[i] = dp[i - 1] * 2 + dp[i - 3]

由于结果可能非常大，所以我们取模 1e9 + 7 来避免溢出。

代码实现

class Solution {
    static int MOD = 1000000007;

    public int numTilings(int n) {
        if (n == 1) {
            return 1;
        }
        long[] dp = new long[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % MOD;
        }
        return (int)dp[n];
    }
}

复杂度分析

• 时间复杂度：O(n)
  只需要线性遍历构造 dp 数组

• 空间复杂度：O(n)
  使用了一个大小为 n+1 的数组存储中间状态，可优化为 O(1) 滚动数组

总结

这题看似复杂，其实本质是一个状态递推的排列计数问题。只要找准状态转移逻辑，就可以写出简洁优雅的动态规划公式。对于我来说，这类题的训练价值在于观察样本、推导递推关系的能力。掌握类似模型（如爬楼梯、分发糖果等），对日常刷题和面试都很有帮助 🧠📈

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。