[LeetCode] 每日一题 3068. 最大节点价值之和（贪心算法）

题目描述

给你一棵 n 个节点的 无向 树，节点从 0 到 n - 1 编号。树以长度为 n - 1 下标从 0 开始的二维整数数组 edges 的形式给你，其中 edges[i] = [ui, vi] 表示树中节点 ui 和 vi 之间有一条边。同时给你一个 正 整数 k 和一个长度为 n 下标从 0 开始的 非负 整数数组 nums ，其中 nums[i] 表示节点 i 的 价值 。

Alice 想 最大化 树中所有节点价值之和。为了实现这一目标，Alice 可以执行以下操作 任意 次（包括 0 次）：

• 选择连接节点 u 和 v 的边 [u, v] ，并将它们的值更新为：

  • nums[u] = nums[u] XOR k

  • nums[v] = nums[v] XOR k

请你返回 Alice 通过执行以上操作 任意次 后，可以得到所有节点 价值之和 的 最大值 。

题目链接

https://leetcode.cn/problems/find-the-maximum-sum-of-node-values

示例输入

示例 1

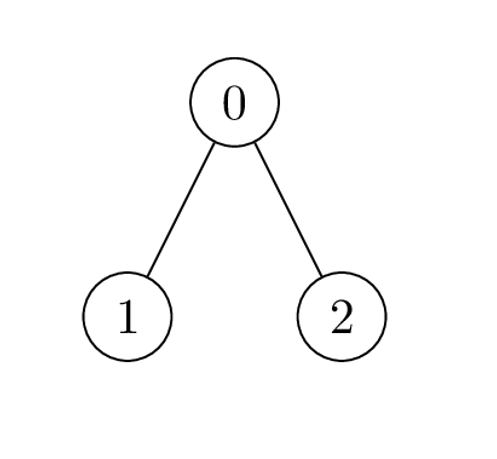
输入：nums = [1,2,1], k = 3, edges = [[0,1],[0,2]]
输出：6
解释：Alice 可以通过一次操作得到最大价值和 6 ：
- 选择边 [0,2] 。nums[0] 和 nums[2] 都变为：1 XOR 3 = 2 ，数组 nums 变为：[1,2,1] -> [2,2,2] 。
所有节点价值之和为 2 + 2 + 2 = 6 。
6 是可以得到最大的价值之和。

示例 2

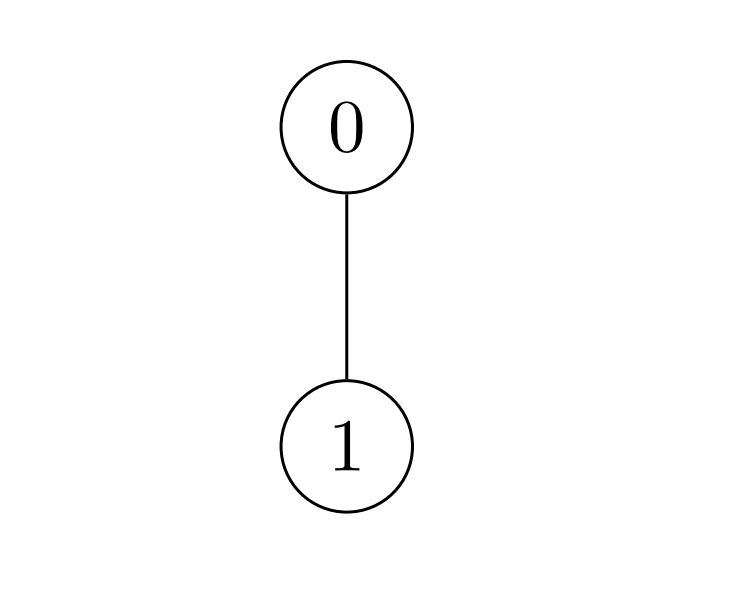
输入：nums = [2,3], k = 7, edges = [[0,1]]
输出：9
解释：Alice 可以通过一次操作得到最大和 9 ：
- 选择边 [0,1] 。nums[0] 变为：2 XOR 7 = 5 ，nums[1] 变为：3 XOR 7 = 4 ，数组 nums 变为：[2,3] -> [5,4] 。
所有节点价值之和为 5 + 4 = 9 。
9 是可以得到最大的价值之和。

示例 3

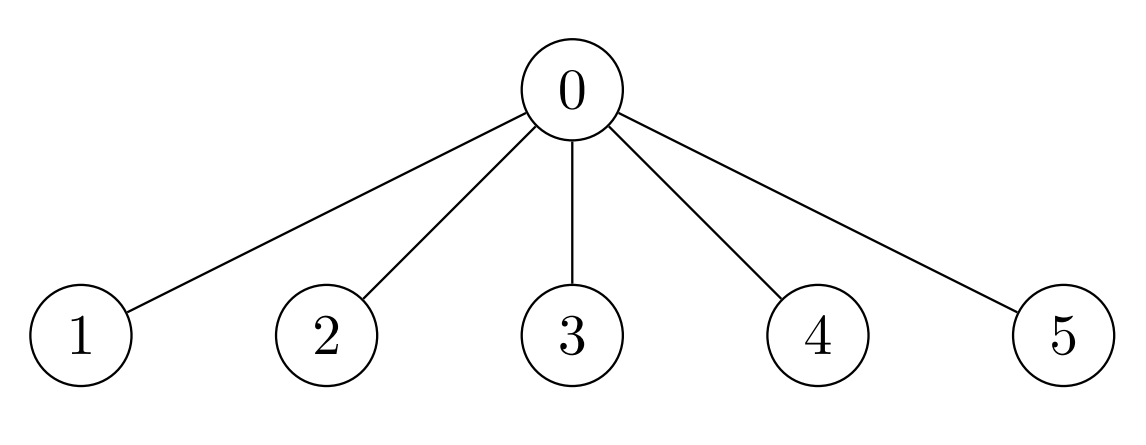
输入：nums = [7,7,7,7,7,7], k = 3, edges = [[0,1],[0,2],[0,3],[0,4],[0,5]]
输出：42
解释：Alice 不需要执行任何操作，就可以得到最大价值之和 42 。

提示

• 2 <= n == nums.length <= 2 * 10^4

• 1 <= k <= 10^9

• 0 <= nums[i] <= 10^9

• edges.length == n - 1

• edges[i].length == 2

• 0 <= edges[i][0], edges[i][1] <= n - 1

• 输入保证 edges 构成一棵合法的树。

解题思路

今天这题第一眼看起来是“树 + 异或”，确实让人感觉信息量挺大。但深入思考你会发现，它的关键并不在于树的结构，而是我们是否能在操作次数上做任意调整。因为给定的是一棵无向树，任意两个节点之间都存在唯一一条路径，所以其实我们是可以通过若干次操作，让任意一对节点异或一次。

于是我们可以得出一个很重要的结论：

我们可以任选任意两个节点来作为一组，使得它们的值同时异或一次 k。

那么问题就变成了：

如何分组，使得异或后的节点总价值尽可能大？

异或的数学性质：

• x ^ k 会对一个数产生某种变化；

• 若 (x ^ k) > x，就意味着我们可以通过异或增加这个数的值；

• 异或操作是可逆的，所以我们最多只能让一个数异或一次。

转化为差值最大化：

我们可以构造一个 diff[] 数组，记录每个节点如果进行一次异或操作后的“收益”：

diff[i] = (nums[i] ^ k) - nums[i]

然后就转化为：在 diff[] 中挑出若干对，使得总收益最大，并且保证每次异或都成对进行（因为每次操作涉及两个节点）。

贪心策略：

1. 先计算所有节点原始的总价值；

2. 计算每个节点异或后的差值 diff[i]；

3. 将 diff[] 按降序排序；

4. 每次尝试取两个 diff 值之和，如果是非负的就加入总价值，否则停止。

这样我们就能用 贪心 + 模拟配对 的方式，选出收益最大的异或组合 🫠🫠

代码实现

class Solution {
    public long maximumValueSum(int[] nums, int k, int[][] edges) {
        long ans = 0;
        int n = nums.length;
        int[] diff = new int[n];
        for (int i = 0; i < n; i++) {
            ans += nums[i];
            diff[i] = (nums[i] ^ k) - nums[i];
        }
        Arrays.sort(diff);
        for (int i = n - 1; i > 0 && diff[i] + diff[i - 1] >= 0; i -= 2) {
            ans += diff[i] + diff[i - 1];
        }
        return ans;
    }
}

复杂度分析

• ⏱️ 时间复杂度：

  • O(n log n)，其中 n 是节点数，排序 diff 数组占主导

• 🧠 空间复杂度：

  • O(n)，用于存储 diff 数组和基本变量

总结

这题的关键不是“树结构”本身，而是“操作自由度”带来的建模转化。一旦我们意识到可以自由配对，就可以将其转化为标准的差值最大化问题。再配合异或的可逆性，我们便能大胆贪心地取最大值对。

是一道典型的“去掉结构复杂性后，抓住本质操作规律”的题 🤗🤗

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。