[LeetCode] 每日一题 1931. 用三种不同颜色为网格涂色（动态规划）

题目描述

给你两个整数 m 和 n 。构造一个 m x n 的网格，其中每个单元格最开始是白色。请你用 红、绿、蓝 三种颜色为每个单元格涂色。所有单元格都需要被涂色。

涂色方案需要满足：不存在相邻两个单元格颜色相同的情况 。返回网格涂色的方法数。因为答案可能非常大， 返回 对 10^9 + 7 取余 的结果。

题目链接

https://leetcode.cn/problems/painting-a-grid-with-three-different-colors

示例输入

示例 1

输入：m = 1, n = 1
输出：3
解释：如上图所示，存在三种可能的涂色方案。

示例 2

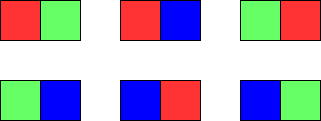
输入：m = 1, n = 2
输出：6
解释：如上图所示，存在六种可能的涂色方案。

提示

• 1 <= m <= 5

• 1 <= n <= 1000

解题思路

说实话，今天这题一上来还挺吓人的，不过一看到数据范围我就意识到关键点在于：m 的范围很小（≤5），而 n 的范围可能很大（最多1000）。这就启发我——我们可以预处理出所有合法的列状态，然后通过动态规划从左到右依次更新。

我一开始就走对了方向，采用三进制的方式来枚举所有可能的列状态（mask），因为每个格子只有 3 种颜色，整个列可以看成一个 m 位的三进制数。

步骤如下：

1. 预处理合法列状态（当前列上下相邻格子颜色不同）

2. 预处理可转移的列状态对（相邻两列每个位置的颜色都不同）

3. 动态规划：定义 dp[i][mask] 表示前 i 列最后一列为 mask 的方案数。状态转移来自所有和 mask 不冲突的前一列状态

4. 因为我们只关心当前列和前一列的状态，所以可以用滚动数组或者 HashMap 节省空间

为了方便管理状态，我使用了 HashMap<Integer, List<Integer>> 来存合法状态及其颜色分布，也用 HashMap 存 dp 表，既方便调试也更直观清晰。

代码实现

class Solution {
    static final int MOD = 1000000007;

    public int colorTheGrid(int m, int n) {
        HashMap<Integer, List<Integer>> vaildMask = new HashMap<>();
        int max = (int)Math.pow(3, m);
        for (int mask = 0; mask < max; mask++) {
            List<Integer> colour = new ArrayList<>();
            int temp = mask;
            for (int i = 0; i < m; i++) {
                colour.add(temp % 3);
                temp /= 3;
            }
            boolean check = true;
            for (int i = 1; i < m; i++) {
                if (colour.get(i).equals(colour.get(i - 1))) {
                    check = false;
                    break;
                }
            }
            if (check) {
                vaildMask.put(mask, colour);
            }
        }
        HashMap<Integer, List<Integer>> canChoose = new HashMap<>(vaildMask.size());
        for (Integer mask1 : vaildMask.keySet()) {
            for (Integer mask2 : vaildMask.keySet()) {
                boolean check = true;
                for (int i = 0; i < m; i++) {
                    if (vaildMask.get(mask1).get(i).equals(vaildMask.get(mask2).get(i))) {
                        check = false;
                        break;
                    }
                }
                if (check) {
                    List<Integer> choices = canChoose.getOrDefault(mask1, new ArrayList<>());
                    choices.add(mask2);
                    canChoose.put(mask1, choices);
                }
            }
        }
        HashMap<Integer, Integer> dp = new HashMap<>(vaildMask.size());
        for (Integer mask : vaildMask.keySet()) {
            dp.put(mask, 1);
        }
        for (int i = 1; i < n; i++) {
            HashMap<Integer, Integer> next = new HashMap<>(vaildMask.size());
            for (Integer mask2 : vaildMask.keySet()) {
                for (Integer mask1 : canChoose.getOrDefault(mask2, new ArrayList<>())) {
                    next.put(mask2, (next.getOrDefault(mask2, 0) + dp.getOrDefault(mask1, 0)) % MOD);
                }
            }
            dp = next;
        }
        int ans = 0;
        for (Integer value : dp.values()) {
            ans = (ans + value) % MOD;
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：

  • O(n s² m)，其中 s 为合法 mask 的数量。主要消耗在每列状态之间的合法性判断和转移

• 空间复杂度：

  • O(s² + s)，用于存储状态之间的合法转移关系和当前 dp 状态

总结

这题是一个状态压缩 + 动态规划的典范，尤其适合 m 小、n 大的网格题目。三进制枚举状态是关键，另外用 HashMap 存储状态能让代码更直观也便于调试。写这题时需要理清楚“列状态”和“状态转移”的概念，一旦理清，整体实现就很顺。

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。