[LeetCode] 每日一题 1007. 行相等的最少多米诺旋转(思考题)
题目描述
在一排多米诺骨牌中,tops[i] 和 bottoms[i] 分别代表第 i 个多米诺骨牌的上半部分和下半部分。(一个多米诺是两个从 1 到 6 的数字同列平铺形成的 —— 该平铺的每一半上都有一个数字。)
我们可以旋转第 i 张多米诺,使得 tops[i] 和 bottoms[i] 的值交换。
返回能使 tops 中所有值或者 bottoms 中所有值都相同的最小旋转次数。
如果无法做到,返回 -1.
题目链接
示例输入
示例 1
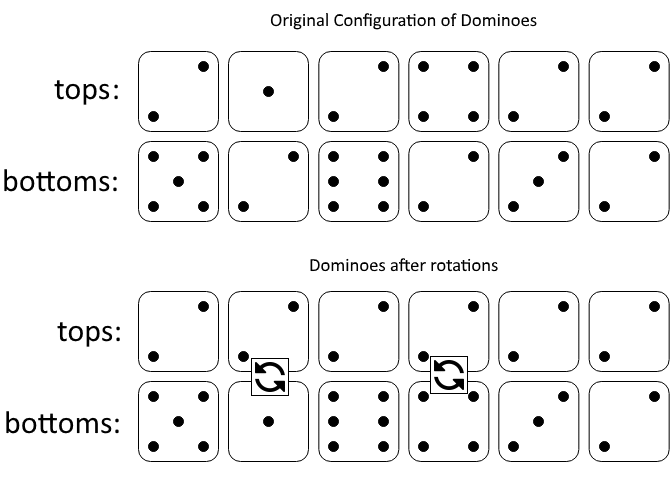
输入:tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2]
输出:2
解释:
图一表示:在我们旋转之前, tops 和 bottoms 给出的多米诺牌。
如果我们旋转第二个和第四个多米诺骨牌,我们可以使上面一行中的每个值都等于 2,如图二所示。 示例 2
输入:tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]
输出:-1
解释: 在这种情况下,不可能旋转多米诺牌使一行的值相等。提示
2 <= tops.length <= 2 * 10^4bottoms.length == tops.length1 <= tops[i], bottoms[i] <= 6
解题思路
这道题其实不是典型的模拟题,而是一道判断可行性 + 目标选择 + 条件计数的组合题,思路上还是比较直接的。我一开始也没有套用什么复杂的算法,而是结合题目本质做了简化。
我们注意到,最终想让 tops 或 bottoms 全部变成同一个值。这个值必然是 tops[0] 或 bottoms[0](否则无法构成全相等)。因此我们可以分别尝试这两个数作为目标值,然后通过一个辅助函数 change 来判断:
如果当前这一位已经是目标值,无需旋转;
如果另一面是目标值,需要旋转一次;
如果两面都不是目标值,说明这个目标根本不可能达成,直接返回
-1。
最终我们对这两种可能情况分别取最小值,得到结果。
代码实现
class Solution {
public int minDominoRotations(int[] tops, int[] bottoms) {
int first = change(tops, bottoms, tops[0]);
if (first == -1) {
return change(tops, bottoms, bottoms[0]);
}
int second = change(tops, bottoms, bottoms[0]);
if (second == -1) {
return first;
}
return Math.min(first, second);
}
private int change(int[] tops, int[] bottoms, int target) {
int top = 0;
int bottom = 0;
int n = tops.length;
for (int i = 0; i < n; i++) {
if (tops[i] != target && bottoms[i] != target) {
return -1;
}
if (tops[i] != target) {
top++;
} else if (bottoms[i] != target) {
bottom++;
}
}
return Math.min(top, bottom);
}
}复杂度分析
时间复杂度:O(n)
尝试两个目标值,每次遍历一次数组,整体是线性时间空间复杂度:O(1)
只用了常数级别的变量计数,没有额外空间开销
总结
这题的核心其实是判断“是否可达”和“哪个更优”。没有过多复杂的数据结构,完全是靠对问题的正确建模和细致的条件判断来解的。我在写的时候也一度担心情况多不好处理,但把目标值限制在 top[0] 和 bottom[0] 后,整个逻辑就非常清晰了。通过这种方式,能训练我们在处理数组题时的目标归纳和条件思维能力,属于典型的“思考题”
希望这篇分享能为你带来启发!如果你有任何问题或建议,欢迎在评论区留言,与我共同交流探讨。