[LeetCode] 每日一题 598. 区间加法 II

题目链接

https://leetcode.cn/problems/range-addition-ii

题目描述

给你一个 m x n 的矩阵 M 和一个操作数组 op 。矩阵初始化时所有的单元格都为 0 。ops[i] = [ai, bi] 意味着当所有的 0 <= x < ai 和 0 <= y < bi 时， M[x][y] 应该加 1。

在 执行完所有操作后 ，计算并返回 矩阵中最大整数的个数 。

示例输入

示例 1

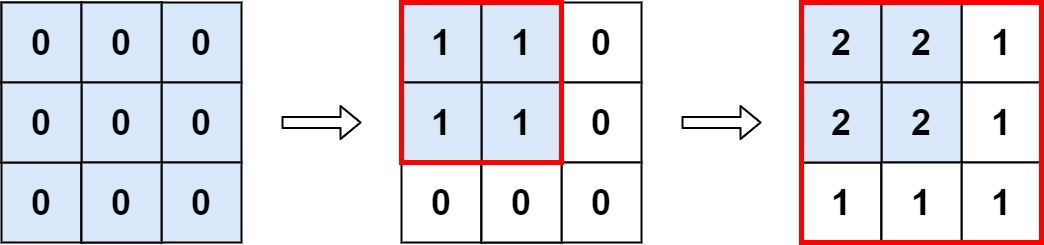
输入: m = 3, n = 3，ops = [[2,2],[3,3]]
输出: 4
解释: M 中最大的整数是 2, 而且 M 中有4个值为2的元素。因此返回 4。

示例 2

输入: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
输出: 4

示例 3

输入: m = 3, n = 3, ops = []
输出: 9

提示

• 1 <= m, n <= 4 * 10^4

• 0 <= ops.length <= 10^4

• ops[i].length == 2

• 1 <= ai <= m

• 1 <= bi <= n

解题思路

本题的目标是计算一个 m x n 的矩阵在执行一系列操作后，矩阵中最大整数的个数。矩阵初始时所有单元格都为 0，每次操作会将一个子矩阵的元素加 1。

关键思路：

• 每次操作都定义了一个子矩阵的右下角 ai, bi，即对 0 <= x < ai 和 0 <= y < bi 的位置进行加 1 操作。

• 因为所有的操作都会影响到矩阵的一部分，我们的任务就是找出最后被操作的最大区域。在所有操作后，矩阵中最大整数的个数显然是矩阵的左上角（即 min(ai) 和 min(bi) 所定义的区域），这个区域中的每个位置都受到了所有操作的影响，并且被加了最多次。

因此，只需要通过对所有操作求出 ai 和 bi 的最小值（即 minX 和 minY），最终矩阵中的最大整数的个数就是 minX * minY。

代码实现

class Solution {
    public int maxCount(int m, int n, int[][] ops) {
        int minX = m;
        int minY = n;
        for (int[] op : ops) {
            minX = Math.min(minX, op[0]);
            minY = Math.min(minY, op[1]);
        }
        return minX * minY;
    }
}

复杂度分析

• 时间复杂度：O(k)，其中 k 是操作数组 ops 的长度。我们需要遍历所有的操作来求最小的 ai 和 bi。

• 空间复杂度：O(1)，只使用了几个额外的变量来存储最小值，空间复杂度是常数级别。

总结

本题的关键是理解操作的影响范围，通过找到所有操作中最小的 ai 和 bi，可以确定矩阵中最大整数的区域大小。由于操作并不改变原始矩阵的形状，求解过程非常简洁，时间复杂度仅为 O(k)，非常高效。通过最小值的计算，我们能快速得出矩阵中最大整数的个数

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。