[LeetCode] 每日一题 59. 螺旋矩阵 II

题目链接

https://leetcode.cn/problems/spiral-matrix-ii

题目描述

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例输入

示例 1

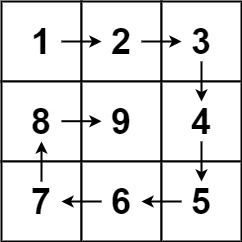
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2

输入：n = 1
输出：[[1]]

提示

• 1 <= n <= 20

解题思路

本题要求生成一个 n x n 的矩阵，元素按顺时针螺旋顺序排列。通过模拟螺旋填充的过程，可以轻松得到答案。核心思路是通过一个方向数组来模拟矩阵中的填充过程，并且每次移动时检查是否可以继续在当前方向前进，若不能则转向

具体步骤如下：

1. 方向数组：使用一个二维数组 dir 来表示四个方向：右、下、左、上

2. 当前位置：使用 x 和 y 变量表示当前位置，初始位置为矩阵的左上角 (0, 0)

3. 填充过程：依次填充矩阵中的每个位置，直到所有位置都被填满。每填充一个位置后，通过判断下一个位置是否越界或已经填充过，决定是否改变填充方向

4. 转向规则：当当前方向无法继续时，按照顺时针方向转向，依次循环右 -> 下 -> 左 -> 上

代码实现

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] ans = new int[n][n];
        // 依次是右下左上
        int[][] dir = { { 1, 0 }, { 0, 1 }, { -1, 0 }, { 0, -1 } };
        // x横坐标,y纵坐标
        int x = 0, y = 0;
        // 初始方向向右
        int d = 0;
        int index = 1;
        while (index <= n * n) {
            ans[y][x] = index;
            index++;
            int nextX = x + dir[d][0];
            int nextY = y + dir[d][1];
            if (nextX < 0 || nextX >= n || nextY < 0 || nextY >= n || ans[nextY][nextX] != 0) {
                d = (d + 1) % 4;
            }
            x += dir[d][0];
            y += dir[d][1];
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：O(n^2)，矩阵的大小是 n x n，因此需要填充 n^2 个位置，每个位置的填充操作是常数时间

• 空间复杂度：O(n^2)，需要一个 n x n 的矩阵来存储结果

总结

这道题本质上是一个经典的模拟题，主要考察对矩阵填充过程的理解。通过使用方向数组模拟顺时针的移动，并通过判断是否越界或已经填充过来决定是否转向，能够顺利实现螺旋填充。整体实现简单直接，适合使用模拟法解决

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。