[LeetCode] 每日一题 2360. 图中的最长环（dfs + 时间戳标记法）

题目链接

https://leetcode.cn/problems/longest-cycle-in-a-graph

题目描述

给你一个 n 个节点的 有向图 ，节点编号为 0 到 n - 1 ，其中每个节点 至多 有一条出边。

图用一个大小为 n 下标从 0 开始的数组 edges 表示，节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边，那么 edges[i] == -1 。

请你返回图中的 最长 环，如果没有任何环，请返回 -1 。

一个环指的是起点和终点是 同一个 节点的路径。

示例输入

示例 1

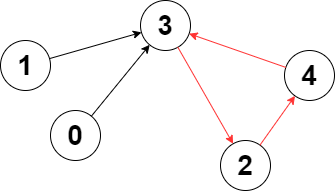
输入：edges = [3,3,4,2,3]
输出去：3
解释：图中的最长环是：2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ，所以返回 3 。

示例 2

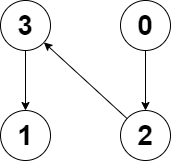
输入：edges = [2,-1,3,1]
输出：-1
解释：图中没有任何环。

提示

• n == edges.length

• 2 <= n <= 10^5

• -1 <= edges[i] < n

• edges[i] != i

解题思路

这道题的本质是找到图中的最长环，并返回其长度。如果没有环，则返回 -1。虽然可以使用 DFS 直接找到环，但会导致重复搜索，影响效率。为了优化，我们可以使用 时间戳标记法，确保每个节点只被访问一次，并记录访问时间，从而计算环的长度。

具体做法如下：

1. 初始化 一个 visit 数组，存储每个节点第一次被访问的时间。

2. 遍历所有节点，对每个未访问的节点进行深度优先搜索（DFS）。

3. 在 DFS 过程中，记录访问顺序，如果遇到已经访问过的节点，则计算时间差，得到环的长度。

4. 更新最长环的长度，最终返回结果。

这样，我们能有效避免重复搜索，同时确保计算出的环长度准确无误🤗

代码实现

class Solution {
    public int longestCycle(int[] edges) {
        int ans = -1;
        int cur = 1;
        int[] visit = new int[edges.length];
        for (int i = 0; i < edges.length; i++) {
            int node = i;
            int start = cur;
            while (node != -1 && visit[node] == 0) {
                visit[node] = cur;
                cur++;
                node = edges[node];
            }
            if (node != -1 && visit[node] >= start) {
                ans = Math.max(ans, cur - visit[node]);
            }
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：O(n) ⏳

  • 每个节点最多访问一次，因此整体时间复杂度为 O(n)

• 空间复杂度：O(n) 💾

  • visit 数组存储访问时间，需要 O(n) 额外空间

总结

这道题的核心是 检测图中的环，并计算最长环的长度。通过 时间戳标记法，我们能够高效记录节点的访问时间，从而避免重复搜索。该方法比直接 DFS 更优，在大规模数据下能显著提升效率

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。