[LeetCode] 每日一题 1206. 设计跳表（非常实用的数据结构）

题目链接

https://leetcode.cn/problems/design-skiplist

题目描述

不使用任何库函数，设计一个 跳表 。

跳表 是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树，其功能与性能相当，并且跳表的代码长度相较下更短，其设计思想与链表相似。

例如，一个跳表包含 [30, 40, 50, 60, 70, 90] ，然后增加 80、45 到跳表中，以下图的方式操作：

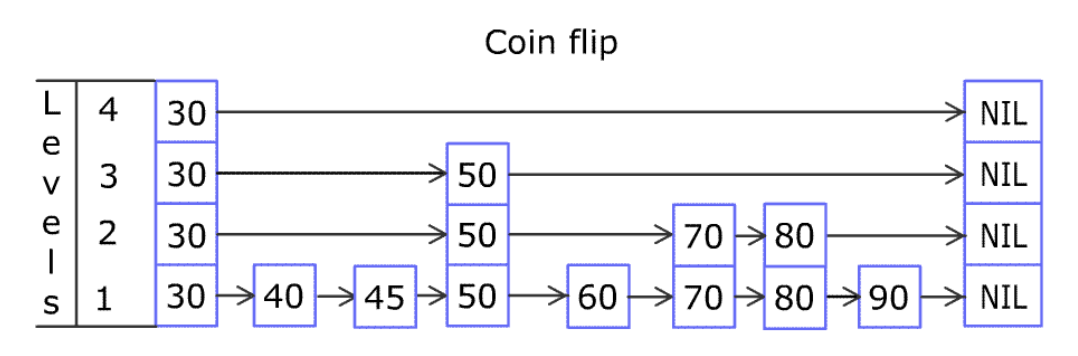
跳表中有很多层，每一层是一个短的链表。在第一层的作用下，增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n))，空间复杂度是 O(n)。

了解更多 : https://oi-wiki.org/ds/skiplist/

在本题中，你的设计应该要包含这些函数：

• bool search(int target) : 返回target是否存在于跳表中。

• void add(int num): 插入一个元素到跳表。

• bool erase(int num): 在跳表中删除一个值，如果 num 不存在，直接返回false. 如果存在多个 num ，删除其中任意一个即可。

注意，跳表中可能存在多个相同的值，你的代码需要处理这种情况。

示例输入

示例 1

输入
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
输出
[null, null, null, null, false, null, true, false, true, false]

解释
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0);   // 返回 false
skiplist.add(4);
skiplist.search(1);   // 返回 true
skiplist.erase(0);    // 返回 false，0 不在跳表中
skiplist.erase(1);    // 返回 true
skiplist.search(1);   // 返回 false，1 已被擦除

提示

• 0 <= num, target <= 2 * 10^4

• 调用search, add,  erase操作次数不大于 5 * 10^4 

解题思路

对于普通的链表，增删改查的操作时间复杂度是 O(n)，这是因为我们需要从头开始遍历链表查找目标元素，性能瓶颈主要出现在查找操作。而跳表通过引入多层链表，显著优化了查找性能

跳表节点结构

对于单链表节点，我们只需要存储当前节点的值和指向下一个节点的指针。而在跳表中，节点不仅存储当前的值，还需要存储在每一层的指针数组 next[i]，其中 next[i] 表示当前节点在第 i 层的下一节点指针。跳表的层数是逐渐递减的，最下层是一个单链表，包含了所有的元素，而更高层则是通过随机选择跳过一些元素来加速查找

查找操作

跳表的查找是从最上层开始，逐层向下进行。当我们在某一层遇到指针为空或指向的元素大于目标值时，就降到下一层继续查找。这种结构使得查找的时间复杂度可以降到 O(log(n))。题目中数据范围最大为 5 * 10^4，因此最多只需要 16 层的跳表就足够了

统一操作：虚拟头节点

为了简化查找操作，我们可以使用一个虚拟头结点 head，其值小于跳表中的任何元素。这样，我们可以通过查找每一层中严格比目标值小的节点来确保后续操作的统一性

操作分解：

• search操作：我们通过查找最后一层，找到最接近目标值的节点，并判断该节点是否为目标值，从而决定是否存在该元素

• add操作：在插入时，从下往上进行插入，最底层一定要插入，然后以 50% 的概率将新节点向上传递

• erase操作：删除时也是从下往上进行，确保删除的是目标元素（需判断是否是同一节点而非相同值的节点），并按层删除

代码实现

class Skiplist {
    static final int DEFAULT_LEVEL = 10;

    static class Node {
        int val;
        Node[] next = new Node[DEFAULT_LEVEL];

        Node(int val) {
            this.val = val;
        }
    }

    private Node head = new Node(-1);
    private Random random = new Random();

    public Skiplist() {
    }

    private void find(int target, Node[] ns) {
        Node cur = head;
        for (int i = DEFAULT_LEVEL - 1; i >= 0; i--) {
            while (cur.next[i] != null && cur.next[i].val < target) {
                cur = cur.next[i];
            }
            ns[i] = cur;
        }
    }

    public boolean search(int target) {
        Node[] ns = new Node[DEFAULT_LEVEL];
        find(target, ns);
        return ns[0].next[0] != null && ns[0].next[0].val == target;
    }

    public void add(int num) {
        Node[] ns = new Node[DEFAULT_LEVEL];
        find(num, ns);
        Node node = new Node(num);
        for (int i = 0; i < DEFAULT_LEVEL; i++) {
            node.next[i] = ns[i].next[i];
            ns[i].next[i] = node;
            if (random.nextInt(2) == 0) {
                break;
            }
        }
    }

    public boolean erase(int num) {
        Node[] ns = new Node[DEFAULT_LEVEL];
        find(num, ns);
        Node node = ns[0].next[0];
        if (node == null || node.val != num) {
            return false;
        }
        for (int i = 0; i < DEFAULT_LEVEL && ns[i].next[i] == node; i++) {
            ns[i].next[i] = ns[i].next[i].next[i];
        }
        return true;
    }
}

复杂度分析

• 时间复杂度：search、add 和 erase 操作的时间复杂度均为 O(log(n))，其中 n 是跳表中的元素个数。因为跳表的高度是通过随机数控制的，平均情况下跳表的层数为 O(log(n))，所以查找、插入和删除操作的时间复杂度均为 O(log(n))

• 空间复杂度：跳表的空间复杂度是 O(n)，其中 n 是跳表中元素的个数。每个节点在每一层都有一个指向下一个节点的指针数组，空间开销取决于跳表的层数和节点数量

总结

最近正好在学习 Redis，在学习过程中接触到了跳表这个数据结构。今天通过这道题，我真正了解了跳表的实现原理。

之前看到过一些关于 Redis 为什么使用跳表而不是红黑树的讨论，其中作者提到说是因为跳表更容易实现。今天我学习实现了一遍跳表，确实发现跳表相较于红黑树实现上更加简单方便，尤其在维护和实践中也显得更为高效。这个过程让我更加明白，在软件工程中，除了要考虑性能之外，工程上的实践性和可维护性也是我们必须综合考虑的关键因素。

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。