[LeetCode] 每日一题 1123. 最深叶节点的最近公共祖先（dfs + 递归）

题目链接

https://leetcode.cn/problems/lowest-common-ancestor-of-deepest-leaves

题目描述

给你一个有根节点 root 的二叉树，返回它 最深的叶节点的最近公共祖先 。

回想一下：

• 叶节点 是二叉树中没有子节点的节点

• 树的根节点的 深度 为 0，如果某一节点的深度为 d，那它的子节点的深度就是 d+1

• 如果我们假定 A 是一组节点 S 的 最近公共祖先，S 中的每个节点都在以 A 为根节点的子树中，且 A 的深度达到此条件下可能的最大值。

示例输入

示例 1

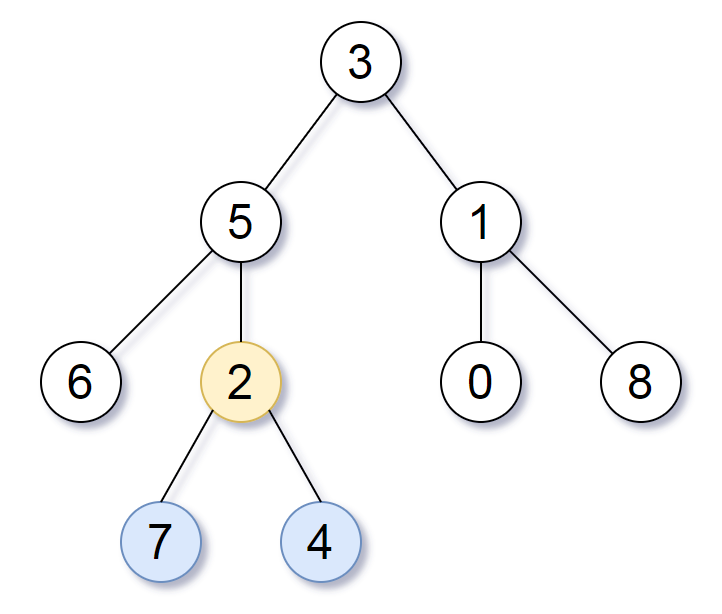
输入：root = [3,5,1,6,2,0,8,null,null,7,4]
输出：[2,7,4]
解释：我们返回值为 2 的节点，在图中用黄色标记。
在图中用蓝色标记的是树的最深的节点。
注意，节点 6、0 和 8 也是叶节点，但是它们的深度是 2 ，而节点 7 和 4 的深度是 3 。

示例 2

输入：root = [1]
输出：[1]
解释：根节点是树中最深的节点，它是它本身的最近公共祖先。

示例 3

输入：root = [0,1,3,null,2]
输出：[2]
解释：树中最深的叶节点是 2 ，最近公共祖先是它自己。

提示

• 树中的节点数将在 [1, 1000] 的范围内。

• 0 <= Node.val <= 1000

• 每个节点的值都是 独一无二 的。

解题思路

今天这道题是关于二叉树中最深叶节点的最近公共祖先，题意不难理解，但需要一些递归的思维

我们可以使用经典的 DFS + 递归 方式来处理
思路如下：

1. 使用 DFS 遍历整棵树，同时传递当前的深度

2. 我们维护一个全局变量 maxDepth，用于记录遍历过程中遇到的最大深度

3. 当我们递归到空节点时，说明已经遍历到了某个路径的末端，此时更新 maxDepth

4. 回溯时，比较左右子树返回的最大深度：

   • 如果左右子树返回的深度都等于 maxDepth，说明当前节点正好是这些最深节点的最近公共祖先，我们将其记录为 ans

5. 最后返回记录下来的 ans 即可

这种写法的核心在于“谁拥有两个最深节点”，谁就是我们要找的那个节点

代码实现

class Solution {
    private TreeNode ans;
    private int maxDepth = -1;

    public TreeNode lcaDeepestLeaves(TreeNode root) {
        dfs(root, 0);
        return ans;
    }

    private int dfs(TreeNode node, int depth) {
        if (node == null) {
            maxDepth = Math.max(depth, maxDepth);
            return depth;
        }
        int left = dfs(node.left, depth + 1);
        int right = dfs(node.right, depth + 1);
        if (left == right && left == maxDepth) {
            ans = node;
        }
        return Math.max(left, right);
    }
}

复杂度分析

• 时间复杂度：O(n)，我们遍历了整棵树，每个节点只访问一次

• 空间复杂度：O(h)，其中 h 是树的高度，主要来自递归栈的深度

总结

这道题让我联想到以往做过的二叉树 LCA（最近公共祖先）问题，只不过这次我们关心的是最深的叶子节点。通过一次 DFS 递归，同时记录最大深度并判断当前节点是否能成为这些最深节点的最近公共祖先，实现起来既简洁又优雅

对于树结构的问题，递归+全局变量的方式在很多场景都很实用，也是我在学习算法中越来越熟练的一种套路 🤗

希望这篇分享能为你带来启发！如果你有任何问题或建议，欢迎在评论区留言，与我共同交流探讨。